Batch 2 - Class 275 - Juice Jumble
Zoom: send meeting Id and password
Start recording
Preclass Exercise:
Mathematics in Pizzeria
In a pizza outlet, they are offering a medium and a small pizza for the same price as a large pizza (the quality, thickness etc are all the same). You do not have a ruler to measure lengths, but happen to have a protractor. How would you decide whether to buy small+medium or the large pizza?
Attendance: Raghav, Aneesh, Kabir, Advay, Shikhar, Ayush, Vivaan, Rhea Chadha, Ryan Chadha, Rohan, Siddanth, Yatharth, Mihir, Dhriti, Anika, Aarkin, Vansh, Tarush, Adyant, Aarushi, Kkushagra, Ekagra, Harshiet, Anshi, Ishita
Class Notes:
Juice Jumble from JRMF
App link https://www.jrmf.org/digitalapps/juice-jumble for students to play with
Use powerpoint for guiding the students through
Strategy for solving any Juice Jumble - Let students think through once they have played around
- Can we go in sequence and first get the first place right, then the second, then the third and so on?
- Students may want to start with smaller problem size
- Can we focus on the empty place and get that right? What if the empty one is at the right place?
- Exchange/ Bubble sort using empty cup to exchange?
- Any other approaches?
- Which of the approaches is faster?
- Do all approaches always work?
- How do you prove that there is always a solution?
How do you think about number of pours
- Students may want to start with smaller problems to solve for this as well
- Is there a pattern in the maximum number of pours required?
- If the cups are in opposite sequence with empty cup at the end, then it seems that 1.5 times the number of colors is required (for odd numbers take the floor with the empty cup being first and then the descending sequence). The pattern is that the empty cup keeps shifting one to the left in each 2 moves, and then after 0.5 of those patterns, all the big numbers are to the right of the cup and fall back in sequence.
- Example 654321E -- 15432E6 -- 1243E56 -- 123E456 --- 123456E (each - denotes a move)
- How do you prove that this is the largest? Can we think recursively about it? For example, can a problem of size n be converted to a problem of size (n-2) with three more steps [for even sized problem?]
- Similarly for odd colors, the worst case is E54321 - by moving once we get 15432E, so a (n-1) sized even problem
- Consider both necessity and sufficiency of the 1.5N moves
Homework Problem:
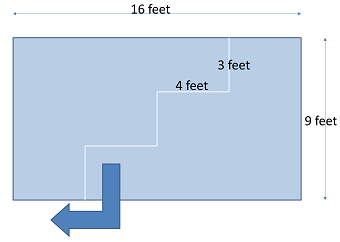
- (Geoffrey - 64) Mr Houseman wishes to lay down carpet on the floor of his kitchen, which is exactly 12 feet x 12 feet. He has a piece of carpet 16 feet x 9 feet, which is just enough to cover the area. However, he doesn't want to cut it in any more pieces that absolutely required. What is the minimum number of pieces he needs to cut the carpet to fit it back on the kitchen floor?
- Answer: 2 pieces
References:
https://docs.google.com/presentation/d/1gNEwvC8yqV79xh-2y2B1sV1kY7ar-_yXul0siKEsgW4/
Mathematical Puzzles, Geoffrey Mott-Smith